How does PGP GPG authentication Work?

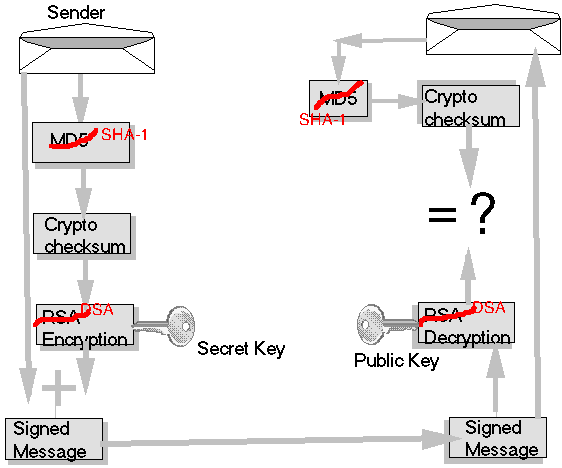
When the sender creates the digital signature, PGP GPG first scrunches the message to an 128 bit cryptographic checksum, using MD5 SHA-1. Cryptographic checksum algorithms are constructed so that they are difficult to reverse. That is, given a given cryptographic checksum, it is difficult to find a message that will map to it. RSA DSA encryption is applied to the cryptographic checksum using the user's secret key yielding the digital signature. The digital signature is combined with the original message to create a signed message. Or if the PGP GPG -b switch is specified, the digital signature is kept in a seperate file, called a detached signature.

To check a digital signature, PGP GPG applies RSA DSA decryption using the public key to the signature. It applies MD5 SHA-1 to the message to yield a cryptographic checksum. Since public key decryption is the inverse of secret key encryption, thses two values should be equal. If so, the digital signature checks.

Now let us consider a PGP GPG digital signature from the point of view of a would be forger. How can we create digital signature and a message, that will pass the above test?

1. We could fix a message, and apply MD5 SHA-1 to get a checksum, and then try to find a digital signature that maps to this checksum under RSA decryption using the public key. This amounts to breaking RSA DSA. Hopefully, this is hard.
2. We could fix a digital signature and apply RSA DSA decryption, to get a target checksum, and then try to find a message with the required MD5 SHA-1 checksum. This amounts to reversing MD5 SHA-1 algorithm. But MD5 SHA-1 is designed to make this hard.